Combining selection of variables with determination of functional relationships for continuous predictors

- the multivariable fractional polynomial approach

So what are fractional polynomials?

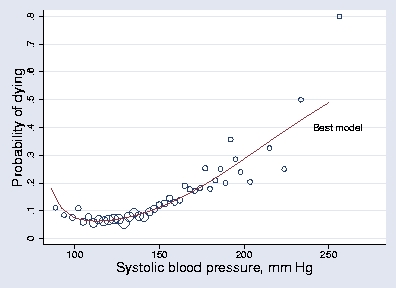
Regression models based on fractional polynomials (FP) functions of a continuous covariate are described by Royston and Altman (1994).

The purpose of FPs is to increase the flexibility afforded by the conventional family of polynomials models. Although polynomials are popular in data analysis, linear and quadratic functions are extremely limited in their range of curve shapes, whereas cubic and higher order curves often produce undesirable artifacts, such as "edge effects" and "waves".

The MFP approach combines the determination of FP functions with backward elimination. It is also possible to incorporate some subject matter preferences. For details see Sauerbrei & Royston (1999), for discription of programms see Sauerbrei, W., Meier-Hirmer, C., Benner, A., Royston, P. (2005): Multivariable regression model building by using fractional polynomials: description of SAS, STATA and R programs, Computational Statistics and Data Analysis, to appear.

For SAS version with documentation and example dataset click here

R-program of MFP: http://www.r-project.org

MFP included in STATA. For contact click here

As an extension to MFP see:
Royston, P. and Sauerbrei, W. (2004). A new approach to modelling interactions between treatment and continuous covariates in clinical trials by using fractional polynomials. Statistics in Medicine 23, 2509-2525

email Patrick Royston (London): Patrick.Royston@ctu.mrc.ac.uk

email Willi Sauerbrei: wfs@imbi.uni-freiburg.de